3.7.2 Solve

This transformation provides a solution to a system of linear equations. The subject is nominally a tuple of linear equations but can also be any expression that conforms to the specification of linear conversion described in §3.6.6.

A solution is found by converting the subject to an augmented matrix, transforming to reduced row-echelon form, and using the variable names provided by the subject to produce a linear system. An example is given in Figure 3.12. Although a similar result can be achieved using a sequence of transformations — linear conversion, reduction and inverse linear conversion — the names of the variables would be lost. Solve does this in one operation, allowing the column names to be preserved.

Parametric conversion (§3.6.7) applied to the same subject as solve performs the same internal transformation but produces a parametric vector instead of a linear system. Like Solve , parametric conversion retains the names of variables in the result.

Subject	Solve	→Parametric
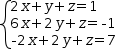(2⋅x+y+z=1, 6⋅x+2⋅y+z=-1, -2⋅x+2⋅y+z=7)ℓ	(x=-1, y=2, z=1)ℓ	(-1,2,1)ʋ
(a+6⋅b+2⋅c-5⋅d=0, -a-6⋅b-c-3⋅d=0, 2⋅a+12⋅b+5⋅c-18⋅d=0)ℓ	(a+6⋅b+11⋅d=0, c+-8⋅d=0)ℓ	(-6⋅b-11⋅d, b, d⋅8, d)ʋ

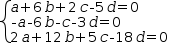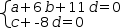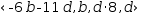Linear and parametric conversions can be mixed with reduction and Solve to achieve a variety of forms. Refer to Figure 3.11.